Abingdon Loop Simulations

Method

The method used for simulating the GPS measurement of the Abingdon 4.5k loop is similar to the methods used to model polygon routes .

1. Way points are positioned along the course so that it can be roughly represented by a number of straight lines. 29 way points defining 28 straight lines do a fair job of representing the course. However on the corners the way points have to be positioned rather wide of the SPR in order to line up with the straight portions of the course. This means that the distance measured on the modelled 28 side polygon will be a little larger than the true distance. However in this model we are not so interested in the absolute distance but rather how much the distance varied with GPS errors in the measurement of wa point location.
2. A the way point locations are modified by adding a random displacement in Eastings and Northings with a Gaussian distribution and a standard deviation of 2.33 m. This is the value of the standard deviation for my ETREX H deduced from measuring way points on Long Tow
3. The distance along the track defined by these modified way points is calculated using Pythagoras.
4. Steps 2 and 3 are repeated 100 times to obtain the standard deviation of the distribution of track lengths.

Way points selected for the model of the Abingdon 4.5 k loop

Result of simulations

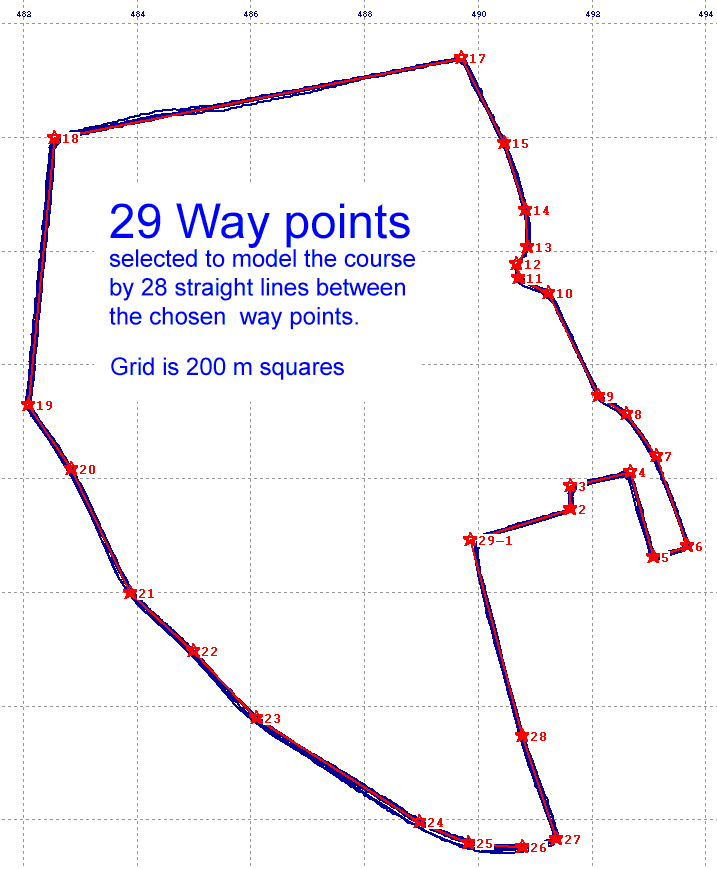
100 simulations of the above model give an average length 4573 m, with a standard deviation of 10 m.

The average length of 4573 m is about 40 m longer than the actual length of the course. This is because the way points did not follow the curves at the apex of a corner but were positioned outside the SPR in order to line up with the straights. A correction could obviously made for this. For example more points could be recorded at the corners, however this could add noise. Alternatively the shape and true distance at the corner could in principle be measured separately and a correction made. However the correction was made, the model provides a lower limit to the error which there will be in the measurement of this course with my GPS which exhibits and standard deviation of 2.33m in each coordinate of a measured way point.

In the next article of this series, the value of 10 m standard deviation obtain from this modelling of GPS measurements of this course will be compared with numbers obtained by riding the course and recording the GPS track or using the GPS's odometer function.

Mike Sandford - 2 April 2009